CONTENTS
Graphs: sine, cosine and tangent
OTHER MATERIAL
Graphs: Sine, Cosine and Tangent
You may have noticed in the previous section some definite relationships between the size of an angle and the values of its trigonometric functions:
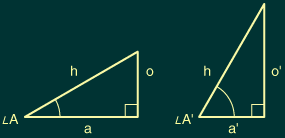
For angles up to 90°, increasing angle A will also increase the length of the opposite side (assuming the hypotenuse stays the same, as shown here). So the sine of angle A will increase as well. At the same time, the adjacent side would become shorter (again, assuming a constant hypotenuse). So the cosine of angle A would actually decrease.
After 90°, the triangle flips horizontally, and the opposite and adjacent sides will start to decrease or increase, respectively:
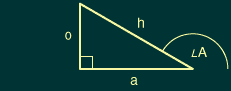
So the sine starts to decrease and the cosine starts to increase. They switch direction again after 180°, and again after 270°. Finally, after 360° the whole pattern repeats—because they're based on angle measurements (which are periodic), the trigonometric functions are periodic.
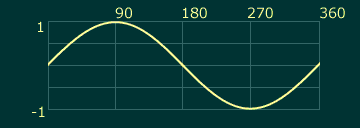
If you were to graph the sine values for angles ranging from zero to 360°, you'd see a rolling wave pattern, AKA a 'sine wave':
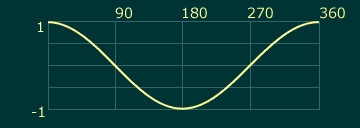
Cosine exhibits a similar pattern, 90 degrees out of phase. You'll notice that when sine is at either extreme (-1 or 1), cosine is zero, and vice-versa:
Tangent displays a strikingly different graph, because its results approach infinity at angles near 90 and 270 degrees. At these angles, the length of the adjacent side becomes increasingly small, while the opposite side approaches the length of the triangle's hypotenuse. As a result, the tangent values start to rapidly approach infinity. Because 'infinity' is not a legal return value, After Effects returns a ridiculously large value for tan(90) or tan(270)—over 5 quadrillion.
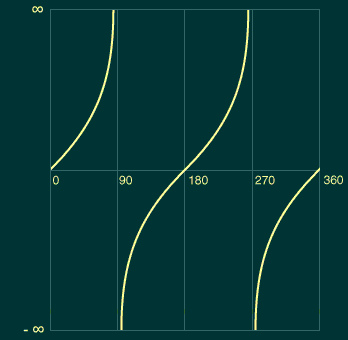
You'll notice that tangent's results change slowly around angles of 0 or 180 degrees, but change rapidly at angles close to 90 or 270 degrees. For instance, from zero to 89 degrees, the tangent increases from zero to only around 57.3; but in that last degree from 89 to 90, the tangent increases from 57.3 to around 5 quadrillion.
You'll also notice that tangent's results are discontinuous—they switch from positive to negative immediately after crossing 90 or 270 degrees. This is because the adjacent side switches direction at these angles.
Finally, tangent's period (the range over which it starts to repeat values) is only 180°.
Interactive Demonstration
Here's a simple project demonstrating how the trigonometric functions
relate to angles. In the project, a solid yellow circle controls the rotation
of a line—in addition to drawing an arc indicating the central angle,
and the opposite and adjacent sides of the corresponding right triangle.
Numeric readouts in the lower corner show the size of the central angle
and the results of these three trigonometric functions.
Click here to download this project. (Windows users click here.)
As you look at this project and the other graphics on this page, you should notice a close relationship between the trigonometric functions and circles. In fact, some older textbooks call these functions 'circular functions'. This is because the set of all right triangles with the same hypotenuse forms a circle, with the hypotenuse defining its radius. We examine this relationship in the next section.