CONTENTS
Graphs: sine, cosine and tangent
OTHER MATERIAL
Distance — Pythagorean Theorem, Length()
There are a variety of reasons you might want to measure the distance between two points—for instance, in a 'span' script, or to create proximity-based effects. As we discussed earlier, you can find the vector between two points simply by subtracting one's position from the other's. The distance between the points is the length of this vector.
There are two basic ways to calculate the length of a vector in After Effects: a hard way, and an easy way. First, the hard way:
Pythagorean Theorem
You may remember the Pythagorean Theorem from high school geometry. It states that, in a right triangle the square of the length of the hypotenuse equals the sum of the squares of the other two sides:
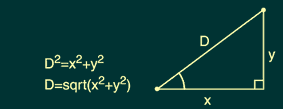
As we discussed earlier, the components of any 2D vector create a right triangle. So we can use the Pythagorean Theroem to calculate the length of the vector between any two points. First, we need to find the vector; then we need to isolate its components. Finally, we can plug these components into the Pythagorean Theorem and get our length.
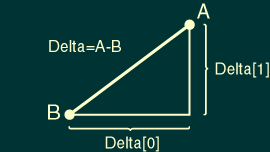
In the Javascript syntax we need for an expression, we'd write:
// Pick 2 points
point1=this_comp.layer("A").position;
point2=this_comp.layer("B").position;
// Find the vector between them
delta=sub(point1, point2);
X=delta[0];
Y=delta[1];
// Now find the length
distance=Math.sqrt(X*X+Y*Y);
This isn't really that hard, but there is an easier way.
length(vector)
After Effects includes a built-in method to calculate the length of any vector: length(). Pass it a vector of any dimension and it will return the length, expressed as a positive number.
Using length(), we could rewrite the above expression:
// Pick 2 layers
point1=this_comp.layer("A").position;
point2=this_comp.layer("B").position;
// Find the vector between them
delta=sub(point1, point2);
// Now find the length
length(delta);
Even though this is only a few lines shorter, this method is much simpler than the Pythagorean Theorem. It also has the advantage of working with vectors of any dimension, such as between 3D layers. We could make the Pythagorean Theorem work in 3D, but it would take some work.
Example: Interactive Blur
![]() So,
what can we do with this length value? Well, one obvious application would
be to control a layer or effect parameter. In this project, we'll use
the interpolation methods to
remap the distance values first to a range appropriate for the Fast Blur
effect, and then to a range appropriate for the Scale parameter.
So,
what can we do with this length value? Well, one obvious application would
be to control a layer or effect parameter. In this project, we'll use
the interpolation methods to
remap the distance values first to a range appropriate for the Fast Blur
effect, and then to a range appropriate for the Scale parameter.
In the first comp, we've applied the Fast Blur effect to four layers. Each of them has the same expression controlling the Blurriness parameter, based on the layer's distance from a control layer (a yellow Solid named "Drag Me"). We use the linear() interpolation method to remap distances of 0 to 80 to a range of 40 to 0. So the blur will be stronger when the control layer is nearby.

After the setup is complete, the animator can simply drag the control layer to interactively blur all four layers, in sequence. The animator can turn off the control layer's video before rendering, without affecting the expression results.
Here is the complete expression. Notice that the only real change from the 'generic' version presented above is the new last line, which uses linear() to remap distance to a more useful range.
// Fast Blur with control layer
// Applied to Blurriness parameter
// Point1 is current layer, point2 is control layer
point1=this_layer.position;
point2=this_comp.layer("Drag Me").position;
// Find the vector between the 2 points
delta=sub(point1, point2);
// Now find the length
distance=length(delta);
//Use linear() to remap distance to range of 40 to 0
linear(distance, 0, 80, 40, 0);
Example: Scale
In the second comp, we've applied the same basic expression to each layer's scale parameter, to create an effect similar to the dynamic scaling seen in the Applications Dock in Apple's MacOS X.

For the most part, we can use the same exact expression as in the first comp, above. Because scale has two components (three for 3D layers), we'll need to rewrite the last line to output a vector instead of just a number. (We discuss arrays and dimensions in more detail here.)
//Remap distance to large scale when near, small when
far
linear(distance, 0, 80, [250,250], [75,75]);
Click here to download this project file. (Windows users click here.)